فيديو: كيف تثبت أن قطري المعين ينصفان بعضهما البعض؟
2024 مؤلف: Lynn Donovan | [email protected]. آخر تعديل: 2023-12-15 23:43
في كل المعين الأضلاع متساوية والأضلاع المتقابلة متوازية. علاوة على ذلك أ معين هو أيضًا متوازي الجرام وبالتالي يعرض خصائص a متوازي الاضلاع وذلك قطري متوازي الأضلاع يشطران بعضهما البعض.
بالمقابل ، هل تنقسم أقطار المعين إلى بعضها البعض؟
في أي معين ، ال قطري (خطوط تربط الزوايا المتقابلة) ينقسم كل منهما الآخر بزاوية قائمة (90 درجة). هذا هو، كل قطري يقطع ال آخر إلى قسمين متساويين ، والزاوية التي يتقاطعان عندها تساوي دائمًا 90 درجة. في الشكل أعلاه ، اسحب أي رأس لإعادة تشكيل معين وتقنع نفسك بهذا.
ثانيًا ، هل الأقطار المعينية متعامدة؟ خصائص أ معين ال قطري نكون عمودي إلى وشطر بعضنا البعض. الزوايا المجاورة مكملة (على سبيل المثال ، A + ∠B = 180 درجة). أ معين هو متوازي الاضلاع ملك من قطري نكون عمودي لبعضهم البعض.
مع وضع هذا في الاعتبار ، كيف يمكنك إثبات أن قطري المعين عبارة عن منصفين متعامدين؟
دليل أن قطري المعين عمودي استمرار أعلاه دليل : الأجزاء المتوافقة من المثلثات المتطابقة متطابقة ، لذا فإن جميع الزوايا الأربع (الزوايا الموجودة في المنتصف) متطابقة. هذا يؤدي إلى حقيقة أنهم جميعًا يساويون 90 درجة و قطري نكون عمودي لبعضهم البعض.
هل المعين متوازي أضلاع؟
التعريف: معين هو متوازي الاضلاع بأربعة جوانب متطابقة. نظرية: إذا أ متوازي الاضلاع هو معين ، كل قطري يشطر زوج من الزوايا المتقابلة. THEOREM Converse: إذا كان a متوازي الاضلاع له أقطار تقسم زوجًا من الزوايا المتقابلة ، فهو a معين.
موصى به:
كيف تثبت عدة اباتشي في لينكس؟
2 إجابات قم بتثبيت Apache على الخادم الخاص بك sudo apt-get install apache2 sudo apt-get install libapache2-mod-perl2 sudo apt-get install other-lib-mods-required. قم بتكوين تكوينات اباتشي منفصلة لكل مثيل تريد تشغيله. قم بتكوين البرامج النصية الأولية لبدء apache بملف التكوين المناسب
كيف أجبر محرك الأقراص المعيّن على الإخراج؟
الطريقة الأولى في نظام التشغيل Windows ، افتح قائمة ابدأ .. افتح مستكشف الملفات .. انقر فوق هذا الكمبيوتر الشخصي. إنه عنصر على شكل كمبيوتر موجود على الجانب الأيسر من نافذة مستكشف الملفات. انقر فوق علامة التبويب الكمبيوتر. انقر فوق Map network drive؟. انقر فوق قطع اتصال محرك أقراص الشبكة. حدد محرك أقراص الشبكة. انقر فوق موافق
كيف تثبت JavaFX في Jgrasp؟
اتبع هذه الخطوات: قم بتنزيل JavaFX SDK من. https://gluonhq.com/products/javafx/ قم بفك ضغط الملف الذي تم تنزيله. افتح المجلد الذي تم فك ضغطه. انسخ هذا المجلد والصقه في مجلد التنزيلات بالداخل. المستخدمون افتح JGrasp. انتقل إلى الإعدادات> PATH / CLASSPATH> مساحة العمل> CLASSPATHS ،
كيف أقوم بتحديد قطري في Photoshop؟
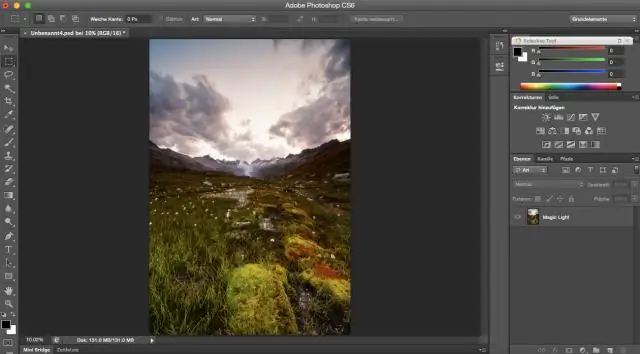
في Photoshop ، اجعل القطع الناقص بالحجم والشكل الذي تريده. بعد ذلك ، انتقل إلى قائمة "تحديد" وحدد "تحديد التحويل" وقم بتدوير / تغيير حجم التحديد. هذا لن يقوم بتدوير / قياس الصورة الأساسية ، فقط التحديد "مسيرة النمل"
ما هي طريقة السلسلة المستخدمة لمقارنة سلسلتين مع بعضهما البعض في C #؟
صيغة الدالة strcmp () هي: بناء الجملة: int strcmp (const char * str1، const char * str2)؛ تُستخدم الدالة strcmp () لمقارنة سلسلتين سلسلتين str1 و str2. إذا كانت سلسلتان متماثلتين ، فإن strcmp () تُرجع القيمة 0 ، وإلا فإنها تُرجع قيمة غير صفرية